作业 (o′┏▽┓｀o)

# 数学思维在密码学中的应用

在进行具体阐述之前，我认为有必要初步介绍一下密码学

# 密码学介绍

我认为密码学要探讨的问题，就是如何更好地进行信息加密、防止信息泄露。
密码学有数千年的历史。最开始为了防止信息泄露，会采取诸如，将信息用特殊的化学墨水写在纸上加以隐藏的手段，

但是这样的保密措施非常容易破解，但凡知道这个方法，就能轻易地读取隐藏地信息。
所以就诞生了密码 —— 一种通过密钥加密信息的手段

# 古典密码

1976 年以前的密码都属于古典密码，
古典密码有很多种，基本地可以大致分为两种，换位密码和替换密码。
简单来说，换位密码就是把明文（需加密的信息）打乱顺序重新排列，而替换密码就是用一张密码表替换明文中的特定字符

# 凯撒密码

以替换密码为例，最简单的替换密码就是移位密码。移位密码，顾名思义就是把 某种字符表 按顺序后移 n 位。这个 n 就是所谓的密钥，而后移之后生成的 新的字符表 就是之前所说的密码表。其中，若是使用以 26 个英文字母（以及 10 个阿拉伯数字）构成的字符表，那么这种密码也被称为凯撒加密。

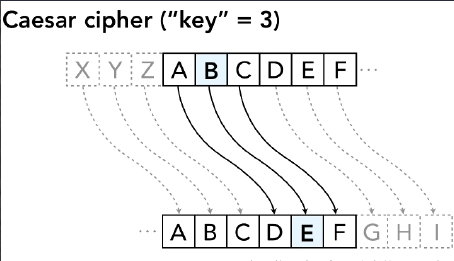
如上图所示，当 n = 3 的时候，即密钥 key = 3，
原字符表为：ABCDE...WXYZ
而密码表为：DEFGH...ZABC

凯撒密码的原理非常简单，对应破解的方式也就非常容易，我们只需要列举出在所有可能的密码表（共 26 种）下解密得到的答案就行了，
毕竟我们能够很清楚地知道，26 种答案里肯定有我们需要的那一个，再要做的，只是读读哪个更加通顺罢了。

# 维吉尼亚密码

因为凯撒密码的破解实在是过于简单，所以在凯撒密码的基础上，诞生了一种新的密码，即维吉尼亚密码，它蕴含的一个思想就是多表替换。
所谓多表替换，就是准备多张密码表，明文的前 n 位选用第 i 张密码表，再后 m 位选用第 j 张... 以此类推，用完所有的密码表之后，就从第 i 张再来过

而维吉尼亚加密，就是准备了 26 张密码表，分别对应凯撒加密的 26 种可能的密码表，依次标记为 ABC...XYZ 。上文的 n 和 m ，在维吉尼亚加密中都是 1，而所有的 i 和 j 对应密码表的标记，组合起来就是密钥。
下表即为维吉尼亚加密的密码表（总）

举个例子，假设明文为 GREAT ，密钥为 GOOD
首先填充密钥使其长度与明文一致，即 GOODG
那么，由 G 对应的密码表（列），找到它的第 G 行，得到第一个密文为 M
然后，由 O 对应的密码表，找到第 R 行，得到第二个密文为 F
同理，我们能获得剩下三个密文为 SDZ，
即，明文 GREAT ，密钥 GOOD 下的维吉尼亚加密结果为 MFSDZ

这样一来，在凯撒密码基础上通过多表替换思想进阶的维吉尼亚密码，对于计算机尚未问世的时代来说，要在未知密钥的情况下强行破解维吉尼亚密码，绝对是一个大工程。

# 对称密码体制和非对称密码体制

# 一。对称加密

对称加密是最快速、最简单的一种加密方式，加密（encryption）与解密（decryption）用的是同样的密钥（secret key）。对称加密有很多种算法，由于它效率很高，所以被广泛使用在很多加密协议的核心当中。自 1977 年美国颁布 DES（Data Encryption Standard）密码算法作为美国数据加密标准以来，对称密码体制迅速发展，得到了世界各国的关注和普遍应用。对称密码体制从工作方式上可以分为分组加密和序列密码两大类。

对称加密算法的优点：算法公开、计算量小、加密速度快、加密效率高。

对称加密算法的缺点：交易双方都使用同样钥匙，安全性得不到保证。此外，每对用户每次使用对称加密算法时，都需要使用其他人不知道的惟一钥匙，这会使得发收信双方所拥有的钥匙数量呈几何级数增长，密钥管理成为用户的负担。对称加密算法在分布式网络系统上使用较为困难，主要是因为密钥管理困难，使用成本较高。而与公开密钥加密算法比起来，对称加密算法能够提供加密和认证却缺乏了签名功能，使得使用范围有所缩小。

对称加密通常使用的是相对较小的密钥，一般小于 256 bit。因为密钥越大，加密越强，但加密与解密的过程越慢。如果你只用 1 bit 来做这个密钥，那黑客们可以先试着用 0 来解密，不行的话就再用 1 解；但如果你的密钥有 1 MB 大，黑客们可能永远也无法破解，但加密和解密的过程要花费很长的时间。密钥的大小既要照顾到安全性，也要照顾到效率，是一个 trade-off。

分组密码：也叫块加密 (block cyphers)，一次加密明文中的一个块。是将明文按一定的位长分组，明文组经过加密运算得到密文组，密文组经过解密运算（加密运算的逆运算），还原成明文组，有 ECB、CBC、CFB、OFB 四种工作模式。

序列密码：也叫流加密 (stream cyphers)，一次加密明文中的一个位。是指利用少量的密钥（制乱元素）通过某种复杂的运算（密码算法）产生大量的伪随机位流，用于对明文位流的加密。解密是指用同样的密钥和密码算法及与加密相同的伪随机位流，用以还原明文位流。

常用对称加密算法包括 DES、3DES、AES

DES（Data Encryption Standard）：数据加密标准，速度较快，适用于加密大量数据的场合。
3DES（Triple DES）：是基于 DES，对一块数据用三个不同的密钥进行三次加密，强度更高。
AES（Advanced Encryption Standard）：高级加密标准，是下一代的加密算法标准，速度快，安全级别高，支持 128、192、256、512 位密钥的加密。

算法特征

加密方和解密方使用同一个密钥。
加密解密的速度比较快，适合数据比较长时的使用。
密钥传输的过程不安全，且容易被破解，密钥管理也比较麻烦。

# 二。非对称加密

非对称加密为数据的加密与解密提供了一个非常安全的方法，它使用了一对密钥，公钥（public key）和私钥（private key）。私钥只能由一方安全保管，不能外泄，而公钥则可以发给任何请求它的人。非对称加密使用这对密钥中的一个进行加密，而解密则需要另一个密钥。比如，你向银行请求公钥，银行将公钥发给你，你使用公钥对消息加密，那么只有私钥的持有人 -- 银行才能对你的消息解密。与对称加密不同的是，银行不需要将私钥通过网络发送出去，因此安全性大大提高。

非对称加密算法的优点：安全性更高，公钥是公开的，秘钥是自己保存的，不需要将私钥给别人。

非对称加密算法的缺点：加密和解密花费时间长、速度慢，只适合对少量数据进行加密。

对称加密算法相比非对称加密算法来说，加解密的效率要高得多。但是缺陷在于对于秘钥的管理上，以及在非安全信道中通讯时，密钥交换的安全性不能保障。所以在实际的网络环境中，会将两者混合使用。

非对称加密算法包括 RSA、Elgamal、背包算法、Rabin、D-H、ECC（椭圆曲线加密算法），常见的有 RSA、ECC。

# 三。分组加密的四种工作模式

# 1.ECB

ECB 模式是最简单的加密模式，明文消息被分成固定大小的块（分组），并且每个块被单独加密。每个块的加密和解密都是独立的，且使用相同的方法进行加密，所以可以进行并行计算，但是这种方法一旦有一个块被破解，使用相同的方法可以解密所有的明文数据，安全性比较差。适用于数据较少的情形，加密前需要把明文数据填充到块大小的整倍数。

ECB 算法优点：
简单、孤立，每个块单独运算。适合并行运算。传输错误一般只影响当前块。
ECB 算法缺点：
同明文输出同密文，可能导致明文攻击。

# 2.CBC

CBC 模式中每一个分组要先和前一个分组加密后的数据进行 XOR 异或操作，然后再进行加密。这样每个密文块依赖该块之前的所有明文块，为了保持每条消息都具有唯一性，第一个数据块进行加密之前需要用初始化向量 IV 进行异或操作。CBC 模式是一种最常用的加密模式，它主要缺点是加密是连续的，不能并行处理，并且与 ECB 一样消息块必须填充到块大小的整倍数。

CBC 算法优点：
串行化运算，相同明文不同密文。
CBC 算法缺点：
需要初始向量。

# 3.CFB

CFB 模式和 CBC 模式比较相似，前一个分组的密文加密后和当前分组的明文 XOR 异或操作生成当前分组的密文。CFB 模式的解密和 CBC 模式的加密在流程上其实是非常相似的。

CFB 算法优点：
同明文不同密文，分组密钥转换为流密码。
CFB 算法缺点：
串行运算不利并行，传输错误可能导致后续传输块错误。

# 4.OFB

OFB 模式将分组密码转换为同步流密码，也就是说可以根据明文长度先独立生成相应长度的流密码。通过流程图可以看出，OFB 和 CFB 非常相似，CFB 是前一个分组的密文加密后 XOR 当前分组明文，OFB 是前一个分组与前一个明文块异或之前的流密码 XOR 当前分组明文。由于异或操作的对称性，OFB 模式的解密和加密完全一样的流程。

OFB 算法优点：
同明文不同密文，分组密钥转换为流密码。
OFB 算法缺点：
串行运算不利并行，传输错误可能导致后续传输块错误。