# 决策树

（Decision Tree）

一种对实例进行分类的树形结构，通过多层判断区分目标所属类别

本质：通过多层判断，从训练数据集中归纳出一组分类规则

优点：

• 计算量小，运算速度快
• 易于理解，可清晰查看各属性的重要性

缺点：

• 忽略属性间的相关性
• 样本类别分布不均匀时容易影响模型表现

# 求解方法

问题核心：属性选择（每一个节点，应该选用哪个属性）

信息熵：

熵是衡量数据集纯度的一个指标（也是度量不确定性的指标）。
对于一个类别变量 C 的数据集 D, 其熵定义为：
$Entropy(D)=-\sum_{i=1}^{n_c}P(c_i)\log_2P(c_i)$
其中，$n_c$ 是类别 C 的个数，$P(c_i)$ 是类别 $c_i$ 在数据集 D 中出现的概率。

纯度：

某次分类中，正确的被分类样本占所有样本的比率。

关键步骤：

1. 属性选择：
   在每个节点上，算法会选择一个最优属性作为分割标准。这一过程可以通过计算不同属性的信息增益（ID3）、信息增益比（C4.5）或基尼不纯度（CART）来进行。

• 信息增益：衡量属性 A 对数据集 D 划分后信息熵减少的程度，表示为：
  $Gain(D,A)=Entropy(D)-\sum_{v=1}^V\frac{|D_v|}{|D|}Entropy(D_v)$
  其中，$V$ 是属性 $A$ 的不同取值个数，$D_v$ 表示在属性 $A$ 上取值为 $v$ 时数据集 $D$ 的子集，$|D_v|$ 和 $|D|$ 分别表示子集和总数据集的样本数量。

• 信息增益比：信息增益与属性固有值的熵之比（因为 ID3 偏向于选择具有较多属性值的属性，可能导致过拟合）。
  $Gain_{ratio}(D,A) =\frac{Gain(D,A)}{H_A(D)}$
  $H_{A}(D) =-\sum_{v=1}^V\frac{|D_v|}{|D|}log_2\frac{|D_v|}{|D|}$
  其中，$H_{A}(D)$ 为属性 A 的固有值（该属性在数据集中包含的信息量）。

• 基尼不纯度：数据集中随机抽取两个样本，它们属于不同类别的概率。

  $Gini(D)=1-\sum_{i=1}^k{(p_i)^2}$

  其中，$p_i$ 是样本属于第 $i$ 类别的概率。

2. 分割数据集：
   根据所选属性的最佳分割点将当前节点下的样本划分为若干子集，并为每个子集生成新的分支节点。

3. 递归建树：
   对于每个新生成的子集节点，重复上述属性选择和分割的过程，直至达到停止条件（如所有样本属于同一类、没有剩余属性可分割或者达到预设的最大深度等）。

4. 停止条件：
   叶节点的最少样本数量 / 最大树深 / 叶节点的最大纯度
   （这会导致某个叶节点中包含多类别的样本：取数量更多的作为叶节点的类别；若并列则随机选一个）

5. 剪枝处理：
   决策树容易过拟合，为了提高泛化能力，通常需要对生成的树进行剪枝操作，移除那些可能带来过拟合影响的复杂分支。
   降低错误剪枝 REP / 悲观错误剪枝 PEP / 基于错误剪枝 EBP / 代价 - 复杂度剪枝 CCP / 最小错误剪枝 MEP

6. 预测阶段：
   构建完成的决策树可以用来预测未知数据的类别或连续值，只需将新数据沿树的路径向下传递，直到到达叶节点，该叶节点对应的类别或数值即为预测结果。

# ID3

• 选择划分依据：
  对于数据集 D 中的每一个属性 A, 计算其信息增益，并从中选择具有最大信息增益的属性作为当前节点的分割依据。

• 生成分支节点：
  根据所选的最佳属性及其各个可能取值，将数据集划分为多个子集。并为每个子集创建新的分支节点。

• 生成叶节点：
  当不能进一步划分时，以该节点下的实例最多的类别作为叶节点的类别标记。

# C4.5

• 选择划分依据：
  信息增益率偏好可取值较少的属性 (分母越小，整体越大)，因此 C4.5 不是直接选取增益率最大的属性，而是使用一个启发式方法：
  先从候选划分属性中找到信息增益高于平均值的属性，再从中选择增益率最高的。
• 处理连续属性：
  （ID3 只能处理离散属性，C4.5 引入了一种将连续属性离散化的方法）
  假设 n 个样本的连续属性 A 有 m 个取值。先将其排序，并取相邻两样本值的中位点作为候选划分点（共 m-1 个），分别计算以候选划分点作为二元分类点（属性 A 上大于 / 不大于划分点的样本集合）时的信息增益，选择信息增益最大的点作为连续属性 A 的二元离散分类点
• 缺失值处理：
  （核心思想：降低缺失值所在样本的权重）
  1. 如何计算信息增益率？
     无视缺失值，先计算剩余样本的信息增益，然后乘以 无缺失值样本所占比例。
  2. 如果选择包含缺失值的属性作为节点，缺失值所在样本应该如何划分到子分支？
     缺失值所在样本按照 无缺失值样本在每个子分支中所占的比例，划分到所有分支中。

# CART

• 既能处理分类问题，也能处理回归问题
• 选择划分依据：
  划分依据为某个属性是否等于某个取值。
  计算每个属性每种取值条件下的基尼不纯度 $Gini(D_a)$，其中 $D_a$ 表示数据集中属性 $A$ 取值 $a$ 下的数据子集，
  选取基尼不纯度最小的取值作为节点的划分依据。
• CART 生成的决策树是二叉树，每个非叶子节点有且仅有两个子节点。
  对于数据集 $D$，个数为 $|D|$，根据属性 $A$ 是否取某一可能值 $a$，把数据集 $D$ 分成两部分 $D_1$ 和 $D_2$，分别表示 取 / 不取 $a$。

# 异常检测

（Anomaly Detection）

根据输入的数据，对不符合预期模式的数据进行识别。

异常检测 => 寻找异常点 => 寻找概率密度值较小的点

概率密度：

1. 用于表示连续型随机变量的概率分布
2. 概率密度函数 $p(x)$ 是一个描述随机变量在某个确定的取值点 $x$ 附近的可能性的函数
3. 区间 $(x_1,x_2)$ 的概率为 $P(x_1,x_2)=\int_{x_1}^{x_2}p(x)dx$
   从 $-\infty$ 到 $+\infty$ 的概率密度函数的积分是 1。

高斯分布

高斯分布的概率密度函数是：

$$p(x)=\frac1{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$

其中，$\mu$ 为数据均值，$\sigma$ 为标准差（大 / 小 => 数据分布离散 / 集中）：

$\mu=\frac{1}{m}\sum_{i=1}^{m}x^{(i)}$；$\sigma^2=\frac{1}{m}\sum_{i=1}^{m}(x^{(i)}-\mu)^2$

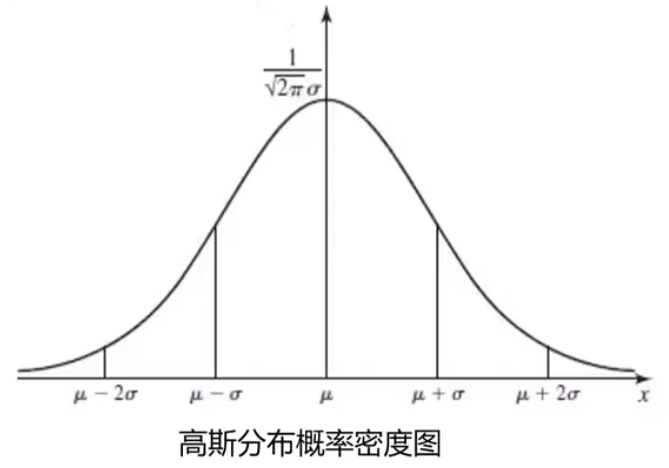
基于高斯分布实现异常检测

数据是一维的情况：（简单理解）
有一维数据：$$\begin {Bmatrix} x_1,x_2,\dots,x_m\end {Bmatrix}$$；共 $m$ 个数据样本

1. 计算数据的均值 $\mu$，标准差 $\sigma$

2. 计算对应的高斯分布概率密度函数 $p(x)$

3. 根据数据的概率密度值，进行判断：
   如果 $p(x_i)<\varepsilon$ ：则 $x_i$ 为异常点

数据是高维的情况：
有高维数据：$$\beginBmatrix}x_1({(1)),x_1^(2)},\dots, x_1({(m))\\dots\x_n^{{(1)},x_n^{(2)},\dots,x_n}\end {Bmatrix}$$；共 $n$ 维，每维有 $m$ 个数据样本。

1. 计算每个维度的数据均值 $\mu_1,\mu_2,...,\mu_n$，标准差$\sigma_1,\sigma_2,...,\sigma_n$

   \begin{array} &\mu_j={\frac{1}{m}\sum_{i=1}^mx_j^{(i)}},&&&\sigma_{j}^{2}=\frac{1}{m}\sum_{i=1}^{m}(x_{j}^{(i)}-\mu_{j})^{2}& \end{array}

2. 计算概率密度函数 $p(x)$：
   分别计算每个维度下的高斯分布概率密度函数， 然后将结果相乘

   $$p(x)=\prod_{j=1}^np(x_j)=\prod_{j=1}^n\frac1{\sigma_j\sqrt{2\pi}}e^{-\frac{(x_j-\mu_j)^2}{2\sigma_j^2}}$$

3. 判断 $p(x_i)<\varepsilon$ ？

# 主成分分析

（PCA） => 降维 => 高维向低维做投影

目标：投影后，不同类别的数据之间 关联度 尽可能小
=> 数据的方差最大（因为方差越大，数据越分散）

计算过程：

• 原始数据预处理：
  （标准化：$\mu=0,\sigma=1$）
• 计算协方差矩阵的特征向量、及数据在各特征向量投影后的方差
• 根据需求（任务指定 或 方差比例）确定降维维度 k
• 选取 k 维特征向量，计算数据在其形成空间的投影