# 线性回归

# 逻辑回归

（用于解决分类问题）

要点：
①寻找决策边界的格式
②损失函数最小化情况下，求解决策边界的系数

分类问题

逻辑回归的简单解释：

sigmoid 函数（一种概率分布函数）$S\left(x\right)=\frac{1}{1+e^{-x}}$ ，图像如下：
其中 S(x) > 0.5 的视为 1， S(x) < 0.5 的视为 0，即可对所有的 x 进行分类。

概率分布函数

$P(x)=\frac{1}{1+e^{-g(x)}}$，其中 $g(x)=0$ 为决策边界（Decision Boundary）， sigmoid 函数就是$g(x)=x$ 的情况。
（所以 $P(x)$ 分类方法同 sigmoid 函数）

$g(x)=\theta_0+\theta_1x_1+\dots$ 为一般格式，可能为多元，包含高次项

损失函数

损失函数 J 即用于评估分类结果的函数。对于不正确的分类结果， J 越大越好；对于正确的分类结果， J 越小越好

因此有 单个样本的损失函数：$\left.J_i=\left\{\begin{matrix}-\log\bigl(P(x_i)\bigr), &y_i=1\\-\log\bigl(1-P(x_i)\bigr), &y_i=0\end{matrix}\right.\right.$

其中 $y_i$ 表示真实结果，$P(x_i)$ 为样本 $x_i$ 的概率分布（预测结果）。

为了在计算机中实现，可将 整体样本的损失函数 等效为：

$\begin{aligned}J&=\frac{1}{m}\sum_{i=1}^{m}J_{i}=-\frac{1}{m}\bigg[\sum_{i=1}^{m}\bigl(y_{i}\log\bigl(P(x_{i})\bigr)+(1-y_{i})\log\bigl(1-P(x_{i})\bigr)\bigr)\bigg]\end{aligned}$

回归问题求解

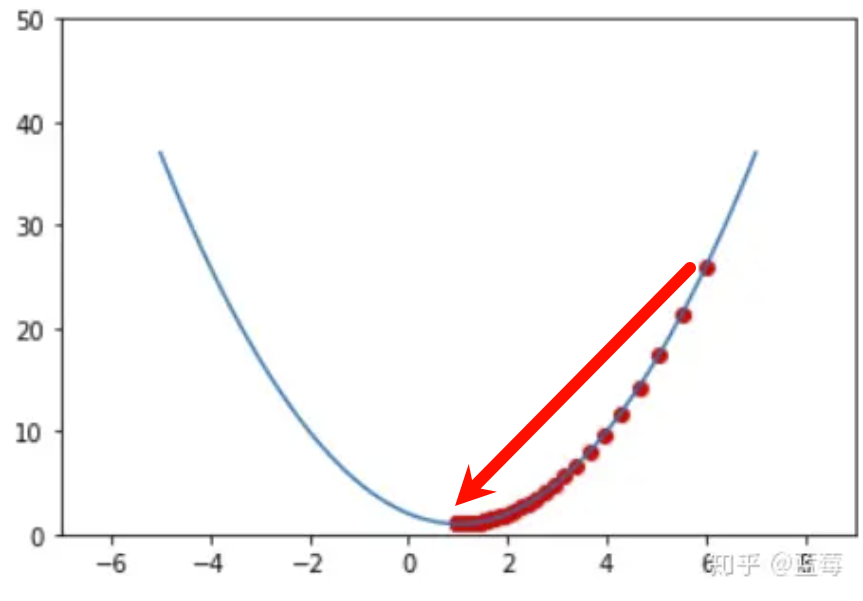
即最小化损失函数：使用梯度下降法，寻找 $min(J)$ 情况下决策边界中 $\theta_i$ 的值。

${\theta_{j+1}}=\theta_{j}-\alpha\frac{\partial}{\partial\theta_{j}}J(\theta)$

每次寻找都为：上一次的结果 + 梯度反方向 × 某一固定值$\alpha$
实际上，每次寻找都会不断接近最优值。