# 无监督学习

不给定带标记的训练示例，自动对输入的数据进行分类或分群。

优点：

1. 算法不受监督信息（偏见）的约束，可能考虑到新的信息
2. 不需要标签数据，极大程度扩大数据样本

主要应用：聚类分析、关联规则、维度缩减

# 聚类分析

又称为群分析，
根据对象的某些属性的相似度，将其自动划分为不同的类别。
（分类问题）

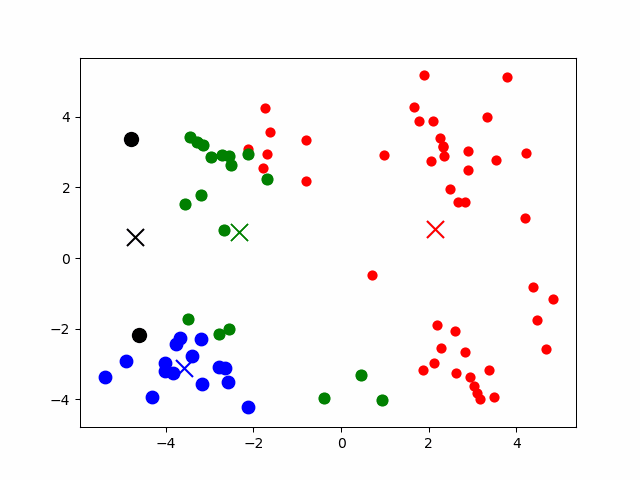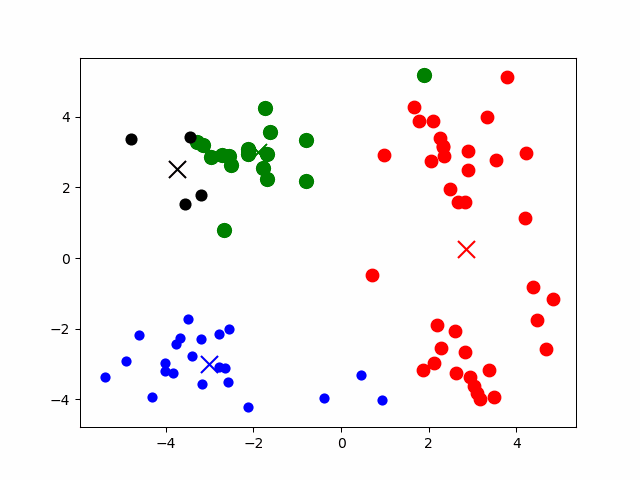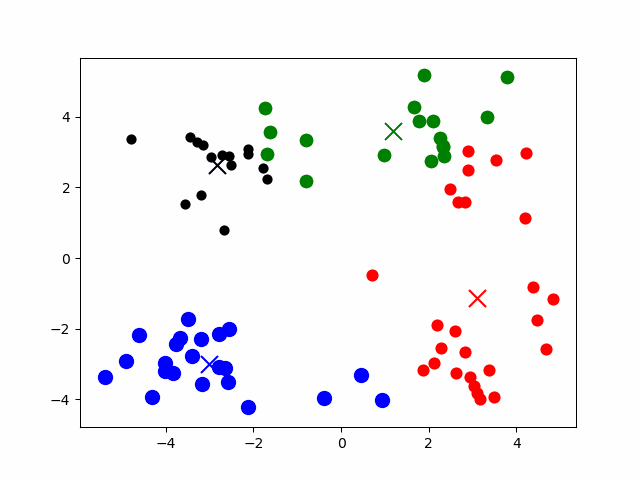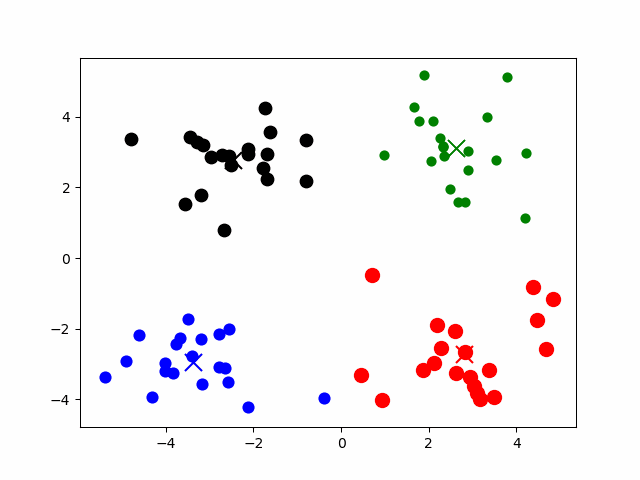
# K-means

K 均值聚类算法：以空间中 k 个点为中心进行聚类，最靠近它们的对象归为一类。

核心步骤：
设 $k$ 个点为 $x_1,x_2,\dots,x_k$，$m$ 个区域簇为 $u_1,u_2,\dots,u_m$
中心点初始值为随机指定的未分类点

• 根据数据与中心点的 距离 划分类别 => 对每个 $x_i$ 计算 $dis(x_i,u_j)$ ，将点 $x_i$ 划入离他最近的区域簇
• 更新中心点为 簇中点的均值 => $u_j = \frac1k\sum_{x_i\in s_j}(x_i)$
• 重复过程直到收敛

特点：
实现简单，收敛快；
但需要指定类别的数量，
且选择的初始中心点不同，结果可能不同，结果可能缺乏一致性。

# KNN

k 近邻分类算法（k nearest neighbor，监督学习算法）

核心步骤：
对于新输入的实例

• 在训练数据集中找到与新实例最接近的 k 个实例
• k 个实例中多数属于某个类，则把新实例归入该类

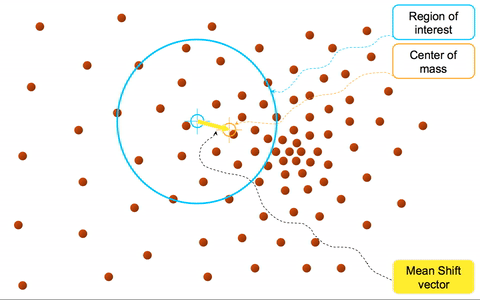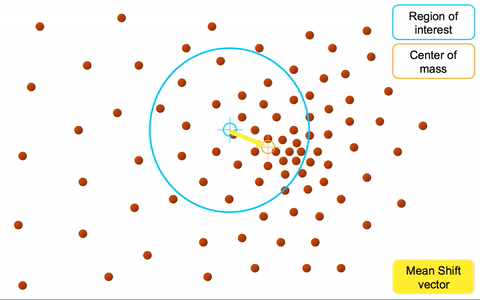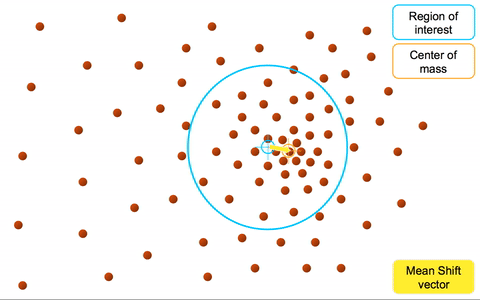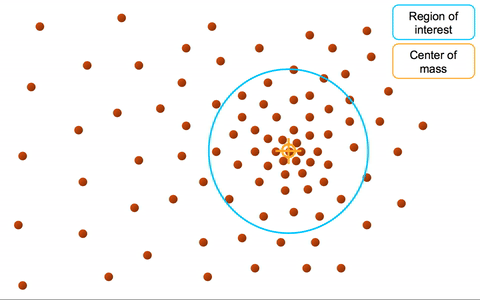
# Mean-shift

均值漂移聚类算法：基于密度梯度上升的算法 => 沿着密度上升方向寻找聚类中心点

核心步骤：
设区域簇 $u$ 内 $k$ 个数据点为 $x_1,x_2,\dots,x_k$，区域簇半径为 $r$
中心点初始值为随机指定的未分类点

1. 在中心点一定半径 ( $r$ ) 的区域内，计算每个数据与中心点偏移的均值 => 均值偏移 $M(x)=\frac{1}{k}\sum_{x_i\in s_h}(u-x_i)$
2. 更新中心点为 原中心点加均值偏移 => $u=u+M(x)$
3. 重复流程到中心点稳定

特点：
不需要人为选择类别数量，但需要指定区域半径（ bandwidth ）

# DBSCAN

基于密度的空间聚类算法

1. 基于 区域点密度 筛选有效数据
2. 基于有效数据向周边扩张，直到没有新点加入

特点：

1. 过滤噪音数据
2. 不需要人为选择类别数量
3. 如果数据密度不同，将影响结果