解决的问题：目标检测和识别、分类和检索、超分辨率重构

核心问题：如何进行 特征提取

---

# 整体架构

卷积神经网络 和 传统网络 的区别：
CNN 的输入数据都是 3 维的，不用拉成一个向量

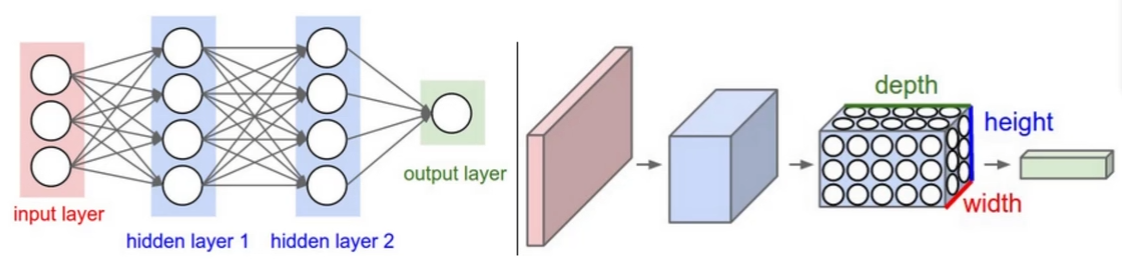
1. 输入层：与传统网络的区别是，直接传入了图像数据（3 维）
2. 卷积层：提取特征
3. 池化层：数据压缩
4. 全连接层：传统神经网络结构；输出层的每一个神经元都与上一层的每一个神经元连接；

每次卷积之后，都会加入一个 Relu 激活函数

卷积层 + 池化层 只是进行特征提取，获得结果还是靠神经网络的全连接层；
因为全连接层无法直接处理 多维 的数据（图像），所以要先把数据拉成 向量 的格式

# 卷积

（提取特征）

关于卷积核 (filter)：参考文章

一次卷积中，

• 假设输入数据有 $n$ 个维度，则卷积核的维度也应当为 $n$（输入数据的每一个维度都对应使用卷积核的一个维度）

• 可以使用多个卷积核。
  每一个卷积核都会对应一个维度的输出数据。假设使用 $m$ 个卷积核，则输出数据将有 $m$ 维。

卷积层涉及参数：

1. 滑动窗口 步长（stride）
   步长越小，越细粒度地提取特征，得到的特征越丰富
   （一般为 1）
2. 卷积核尺寸
   尺寸越小，越细粒度地提取特征，得到的特征越丰富
   （最小为 $3\times 3$）
3. 边缘填充（pad）
   为解决 边界数据利用不充分 的问题（靠近中心的数据在卷积中会被计算更多次），
   在数据边缘填充一圈 0，使数据更靠近中心
4. 卷积核个数
   即输出数据（特征图）的维度
   （每个卷积核都会 各自 进行参数更新）

卷积结果计算公式：

• 长度：$H_2=\frac{H_1-F_H+2P}s+1$
• 宽度：$W_2=\frac{W_1-F_W+2P}s+1$

其中，$W_1$、$H_1$ 表示输入的宽度、长度；$W_2$、$H_2$ 表示输出特征图的宽度、长度；
$F$ 表示卷积核长和宽的大小；$S$ 表示滑动窗口的步长；$P$ 表示边界填充 (加几圈 0)。

所以特征图的大小 不一定 小于输入数据的大小。通过更改卷积的参数，也可以让输入输出的数据大小相同

# 池化

（数据压缩）

关于池化 (pooling)：参考文章

max pooling：选取区域内最大的

average pooling：选取区域内的平均值（已淘汰）

没有矩阵计算（所以池化层不算入卷积神经网络的一层）

池化在压缩数据的同时，势必会导致部分信息丢失，因此可以考虑在下一层卷积中，将特征图个数翻倍，以弥补损失。

# 特征图变化

卷积 => 提取特征 => 增加（减少）特征图个数

池化 => 数据压缩 => 减少特征图体积

转化 => 把 $n$ 个特征图 ($w\times h\times n$) 转化为特征向量 ($(w+h+n)\times 1$)

# 残差网络

问题：神经网络的层数越多，效果越好吗？
不是的
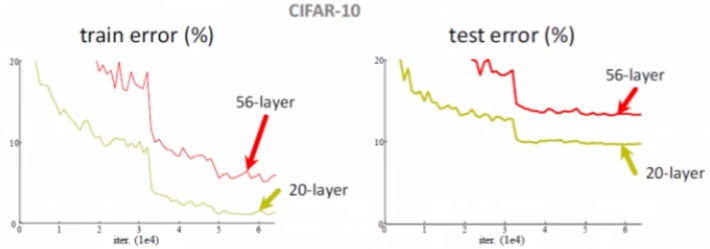
本质上神经网络中间的几层都是在做特征提取的事情，而提取 50 次特征不一定比提取 20 次特征的效果好

** 因此，深度学习出现了如下图所示的状况： **

（ResNet：2015 年提出的解决方法）

核心思想：始终保留增加的层，即使增加的层表现得不好（损失值变大），将