首页Graduation深度学习

# 神经网络基本原理

解决的问题：特征提取（哪些特征比较合适）
应用：检测、识别

# 前向传播

前向传播：得出损失值

image-20240203135000064
（其中 xx 为输入数据，WW 为权重参数，LL 为损失值)

# 得分函数

线性函数：从输入 -> 输出的映射
其结果表示输入数据对于每个分类的得分。

数学表示：
f(x,W)=Wx (+b)f(x, W)=Wx\ (+b)
其中 xx 为图像，WW 为权重参数，bb 为偏置参数。
通常 WW 对结果起决定作用，bb 对结果起微调作用；

假设图片为 [32×32×3][32\times32\times3]，共有 10 个分类，
则 xx 为 3072×13072\times1, WW 为 10×307210\times3072, bb 为10×110\times1, 最终结果为 10×110\times1；
表示该图像分别对这 10 个分类的得分。

深度学习其实就是在寻找最优的 WW

# 损失函数

衡量 分类的结果 和 真实情况 之间的差距。

损失函数 = 数据损失 + 正则化惩罚项

数据损失 (Data Loss)：数据 造成的损失

例如 Li=∑j≠yimax⁡(0,sj−syi+1)L_{i}=\sum_{j\neq y_{i}}\max(0,s_{j}-s_{y_{i}}+1)，
其中 yiy_i 表示真实的分类结果

image-20240203132520467

则 L1=max⁡(0,5.1−3.2+1)+max⁡(0,−1.7−3.2+1)=2.9L_1=\max(0,5.1-3.2+1)+\max(0,-1.7-3.2+1)=2.9
L2=max⁡(0,1.3−4.9+1)+max⁡(0,2−4.9+1)=0L_2=\max(0,1.3-4.9+1)+\max(0,2-4.9+1)=0
L3=max⁡(0,2.2+3.1+1)+max⁡(0,2.5+3.1+1)=10.9L_3=\max(0,2.2+3.1+1)+\max(0,2.5+3.1+1)=10.9

正则化惩罚项：权重参数 WW 造成的损失（与数据无关）
λR(W)=λ∑k∑lWk,l2\lambda R(W)=\lambda \sum_k\sum_l W_{k,l}^2，
其中 λ\lambda 为惩罚系数，越大表示越不希望发生过拟合

Softmax 分类器

（分类问题，因为要的是概率值）

由 得分值 获得 概率值，再将其转化为 损失值

  1. 放大 得分值之间的 差异 ：(exe^x)
  2. 归一化： (P(Y=k∣X=xi)=esk∑jesj{P(Y=k|X=x_{i})=\frac{e^{s_{k}}}{\sum_{j}e^{s_{j}}}}，s=f(xi,W)s=f(x_i,W))
  3. 计算损失值： (Li=−log⁡P(Y=yi∣X=xi){L_i=-\log P(Y=y_i|X=x_i)})

# 反向传播

反向传播：优化模型（找到使 损失值 最小的 WW）

梯度下降算法：判断损失值是否达到最小，否则进行优化：W=W+梯度反方向×某一固定值αW=W+梯度反方向\times某一固定值 \alpha

反向传播遵循链式法则：梯度是从后往前、逐层传播的

沿着输出层的 输出结果 的计算顺序的 倒序 进行反向传播
=> 比如 [(x⋅W1)⋅W2]⋅W3[(x\cdot W_1)\cdot W_2]\cdot W_3，则反向传播时 先计算 W3W_3 的梯度。

整个过程可以划分出多个门单元：

  1. 正向传播中，下一门单元的输入数据 为 上一个门单元的输出数据
  2. 反向传播从最后一个门单元开始，当前门单元的梯度=当前门单元的梯度计算值×后面门单元传递来的梯度当前门单元的梯度 = 当前门单元的梯度计算值 \times 后面门单元传递来的梯度

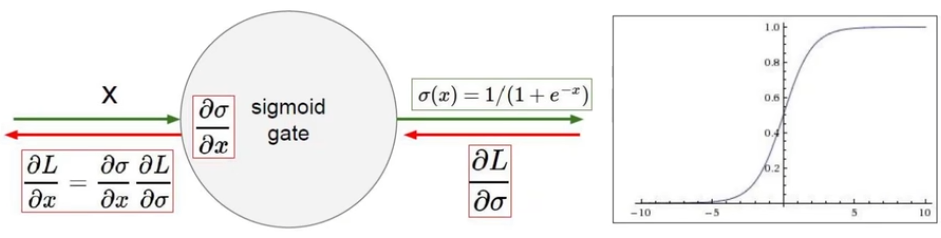
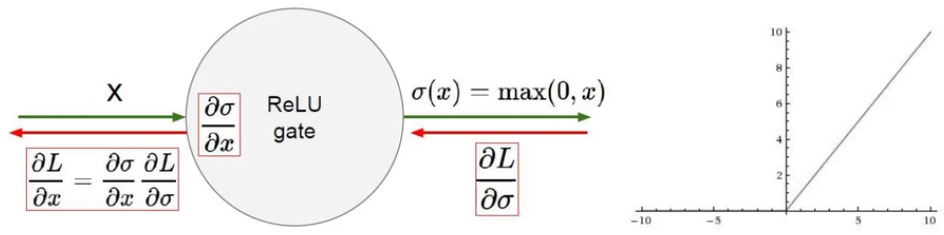
如下图，红框中的部分就是一个门单元；
箭头上方的绿色部分为前向传播的内容，表示当前门单元的输出（也是下一个门单元的输入）；
箭头下方的红色部分为反向传播的内容，表示上一个门单元计算得到的梯度。

image-20240203201632095

门单元：（一种操作）

  1. 加法门单元：
    对于 x+y=qx+y=q，因为 qq 对 xx 和 yy 求偏导的值都是 1，所以 xx 和 yy 向后传播的梯度不变。
    (后面传来的梯度会均匀地分给 xx 和 yy )
  2. 乘法门单元：
    对于 x×y=qx\times y=q，因为 qq 对 xx 求偏导为 yy，对 yy 求偏导为 xx ，所以 x向后传播的梯度=后面传来的梯度×yx向后传播的梯度=后面传来的梯度\times y
    (互换)
  3. MAX 门单元：
    后面传来的梯度 只会 传递给输入值 最大的 那一项，其余小的项的梯度均为 0。

# 整体架构

image-20240203224749357

  • 层次结构：神经网络是分层的。每一层在前一层的基础上 对数据进行变换。

  • 神经元：数据的特征数量。比如输入层有 3 个神经元，其实表示输入数据为 [n,3][n,3] 的矩阵，即存在 3 个特征。
    （隐藏层 1 中有 4 个特征，隐藏层 2 同理）

  • 全连接：对于中间的每一层的神经元，都与前一层每个神经元连接起来。
    （连接：权重参数矩阵，如上图 W1W_1 为 [3,4][3,4]，W2为[4,4]W_2为[4,4]，W3为[4,1]W_3为[4,1]）

  • 非线性：与进入下一层之前，要先将数据带入一个非线性函数（激活函数）。
    （并不是直接进行矩阵乘法得到下一层）

神经元个数越多，得到的拟合程度越大，在训练集上得到的效果越好，但运行速度也越慢，过拟合风险也越大

# 激活函数

在进入下一层之前，需要将结果带入 激活函数（activation function）
image-20240204103909908

常用的激活函数：

  • Sigmoid
    image-20240204104322221
    存在问题：（因此不怎么使用)
    • 梯度消失：因为某一步操作导致梯度为 0
      （因为梯度下降算法是乘法操作，如果某一步梯度为 0，则后续都不会进行更新）。
      Sigmoid 函数最左和最右侧的点，梯度约等于 0。
  • Relu
    image-20240204105235840
    最常用的激活函数
  • Tanh
  • ...

# 数据预处理

  1. 中心化（获得 zero-centered data） => 每个数据减去均值
  2. 维度放缩（获得 normalized data） => 每个数据除以标准差

image-20240204153409550

# 参数初始化

（初始化 权重参数矩阵）

通常使用 随机策略 进行参数初始化：W=0.01×np.random.randn(D,H)W=0.01 \times np.random.randn(D,H)

乘以 0.01 的原因：
我们希望 WW 中的数据 浮动较小（浮动较大的模型更容易导致过拟合）

# 过拟合解决方法

  1. 正则化惩罚项（损失函数中加入 λR(W)\lambda R(W) 项）
  2. DROP-OUT（七伤拳）
  3. ...

DROP-OUT：
在 每一次 的神经网络的训练过程中，对每一层都随机地杀死一些神经元
（每次 不使用 的神经元都是随机的）
image-20240204155147233